Методические рекомендации к изучению теоретического материала темы «Арифметическая и геометрическая прогрессии»

Полезно обратить внимание учащихся на то, что натуральные числа образуют арифметическую прогрессию с разностью, равной 1 и : 1, 2, 3, 4 . .

Геометрическая прогрессия по определению также представляет собой последовательность, задаваемую следующим рекуррентным соотношением: , т.е. задается условиями: и .

Первое знакомство учащихся с прогрессиями (как арифметической, так и геометрической) можно начать с конкретных примеров нескольких последовательностей, среди которых имеются, например, арифметические прогрессии. Рассматривая эти примеры, учащиеся могут выявить характеристические свойства последовательностей некоторого вида, которые учитель затем называет арифметическими прогрессиями и предлагает учащимся самостоятельно сформулировать определение такой прогрессии.

Следует указать учащимся, что любую постоянную последовательность, каждый член которой принимает значение, равное числу с, можно рассматривать и как арифметическую прогрессию с разностью , и как геометрическую прогрессию со знаменателем q = 1.

В зависимости от значения разности прогрессии d (или знаменателя прогрессии q) характер поведения членов прогрессии различен. Так, арифметическая прогрессия будет возрастающей, если , и будет убывающей, если d < 0.

Несколько сложнее обстоит дело с геометрической прогрессией. Поэтому характер поведения геометрической прогрессии в зависимости от значений q следует разобрать с учащимися более детально, например, по такому плану:

1) Пусть q > 1, тогда члены геометрической прогрессии таковы, что их значения имеют один и тот же знак и возрастают по модулю.

Пример 1. 1, 3, 9, 27, 81, . (т. е. , q = 3), или – 2, – 8, – 32, . (т. е. ).

2) Если , то члены геометрической прогрессии таковы, что их значения имеют один и тот же знак и убывают по модулю.

Пример 2. 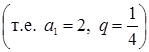, или .

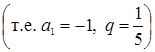3) Пусть , тогда члены геометрической прогрессии принимают знакочередующиеся значения, возрастающие по модулю,

Пример 3. – 3, 6, – 12, 24, . .

4) Если , то члены геометрической прогрессии принимают знакочередующиеся значения, убывающие по модулю.

Пример 4. – 8, 1, .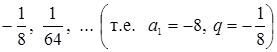

5) При q = 1 все члены геометрической прогрессии одинаковы, т. е. , а при все члены геометрической прогрессии отличаются друг от друга лишь знаками, т.е. [17].

Остановимся теперь на выводе формулы общего члена прогрессии. Опыт работы преподавателей показывает, что вывод формул общего члена арифметической и геометрической прогрессий не вызывает затруднений у учащихся, поэтому в классе работу по выводу формул общего члена арифметической и геометрической прогрессий можно провести на уроке-лекции по введению и самостоятельному приобретению новых знаний «Сравнение арифметической и геометрической прогрессий» самостоятельно по вариантам, а затем сделать вывод и записать формулы и . На этом же уроке учитель подводит учащихся к характеристическим свойствам прогрессий с помощью трех заданий, предлагаемых ученикам последовательно.

1) Найти среднее арифметическое (геометрическое) чисел 2 и 8. Записать найденное число с данными в порядке возрастания. Образуют ли эти числа арифметическую (геометрическую) прогрессию?

2) Справедлива ли эта зависимость для трех последовательных членов рассматриваемых последовательностей?

а) (для арифметической прогрессии);

б) (для геометрической прогрессии).

3) Доказать, что для членов прогрессий справедлива закономерность:

Другие статьи:

Экспериментальное исследование сформированности экологических знаний у детей старшего дошкольного возраста
Для более комплексного исследования проблемы экологического образования дошкольников, в работе были применены следующие методы исследования: теоретический анализ и обобщение; педагогический эксперимент. В ходе педагогического эксперимента был использован метод педагогического тестирования. Педагогический экс ...

Влияние обучения на образовательную и педагогическую деятельность студентов
Для исследования адекватности учебного процесса был проведён опрос субъективного мнения студентов об отношении к организации учебного процесса. Рис 18. Удовлетворенность организацией учебного процесса Обследование по удовлетворённости организацией учебного процесса (рис. 18) показало, что студенты в 62% орга ...

Главные разделы

• Главная
• Профессиональное самоопределение школьников
• Воспитание этнической толерантности в школе
• Понятие и технология обучения
• Образовательные технологии
• Оптимизация системы образования
• Изучение информационных технологий в школе
• Педагогика как наука