Арифметическая прогрессия

Пример 2. Если и d = 2, то получим арифметическую прогрессию: 1; 3; 5; 7; 9; … , которая является последовательностью положительных нечетных чисел.

Пример 3. Если и , то заданная арифметическая прогрессия: – 2; – 4; 0; 8; 10; … является последовательностью отрицательных четных чисел.

Пример 4. Если и , то имеем арифметическую прогрессию: 7; 7; 7; … , все члены которой равны между собой.

Зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т. д. члены. Но для нахождения члена прогрессии с больший номером такой способ неудобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.

По определению арифметической прогрессии

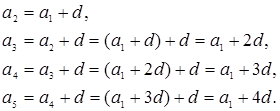
Точно так же находим, что , и вообще, чтобы найти нужно к

прибавить (n – 1)d, т. е.

(2)

Мы получили формулу n

-го члена арифметической прогрессии

. Докажем ее методом математической индукции.

1. При эта формула верна: .

2. Предположим, что формула (2) верна при , , т.е.

3. По определению арифметической прогрессии . Подставляя сюда выражение для k-го члена, получим , а это есть формула (2) при .

Из принципа математической индукции следует, что формула (2) верна для любого натурального п.

Что и требовалось доказать.

Приведем примеры решения задач с использованием этой формулы.

Пример 1. Последовательность – арифметическая прогрессия, в которой и . Найдем десятый и сотый член этой прогрессии.

Имеем:

Пример 2. Выясним, является ли число 71 членом арифметической прогрессии : – 10; – 5,5; – 1; 3,5; . .

В данной арифметической прогрессии и , . Запишем формулу n-го члена прогрессии:

, т.е. .

Число 71

является членом арифметической прогрессии , если существует такое натуральное числи n, при котором значение выражения (4,5n – 14,5) равно 71. Решим уравнение 4,5n – 14,5 = 71.

Получим: 4,5n = 85,5, п=19.

Значит, число 71 является членом данной арифметической прогрессии.

Формулу n-го члена арифметической прогрессии можно записать иначе:

Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида , где k и b – некоторые числа.

Верно и обратное: последовательностъ , заданная формулой вида , где k и b – некоторые числа, является арифметической прогрессией.

Действительно, найдем разность (n+1)-го и n-го членов последовательности :

Другие статьи:

Концепция проблемного обучения
Концепция проблемного обучения связана с интенсификацией традиционного обучения, что предполагает поиск резервов умственного развития учащихся и, прежде всего, – творческого мышления, способности к самостоятельной познавательной деятельности. Разработка концепции обусловлена тем, что в последние годы быстро ...

Программы коррекции педагогической запущенности
Коррекционная программа для клиента №1 1. Нормативно-правовая основа программы. Конвенция ООН о правах ребенка Конституция Российской Федерации 2. Цели программы: · Искоренить недостатки нравственного развития, способствовать вовлечению детей в полноценную жизнь и деятельность ученического коллектива. · Обуч ...

Главные разделы

• Главная
• Профессиональное самоопределение школьников
• Воспитание этнической толерантности в школе
• Понятие и технология обучения
• Образовательные технологии
• Оптимизация системы образования
• Изучение информационных технологий в школе
• Педагогика как наука