Геометрическая прогрессия
Пример 3. Найдем сумму шести первым членов геометрической прогрессии ![]() , если известно, что
, если известно, что ![]() и
и ![]() .
.
Зная ![]() и
и ![]() , можно найти знаменатель прогрессии q.
, можно найти знаменатель прогрессии q.
Так как ![]() то
то 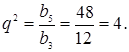
Значит, ![]() или
или ![]()
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.
Если ![]() , то
, то 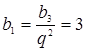
![]() и
и 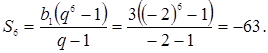
Если ![]() , то
, то ![]() и
и 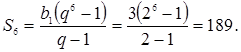
Мы знаем, что число ![]() обращается в бесконечную десятичную периодическую дробь 0,3333 . .
обращается в бесконечную десятичную периодическую дробь 0,3333 . .
Если по аналогии с конечной десятичной дробью разложить бесконечную десятичную дробь 0,3333… по разрядам, то получим сумму с бесконечным числом слагаемых: 0,03 + 0,003 + 0,0003 + . .
Слагаемые в этой сумме являются членами геометрической прогрессии 0,3; 0,03; 0,003; 0,0003; ., у которой ![]() .
.
По формуле суммы n первых членов геометрической прогрессии имеем:
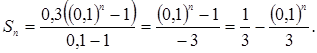
При неограниченном увеличении числа слагаемых n выражение ![]() становится сколь угодно близким к нулю, а значит, и вся дробь
становится сколь угодно близким к нулю, а значит, и вся дробь ![]() неограниченно приближается к нулю.
неограниченно приближается к нулю.
Действительно, если n = 2, то 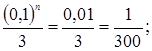 если n = 3, то
если n = 3, то 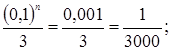 если n = 4, то
если n = 4, то 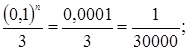 если n = 5, то
если n = 5, то 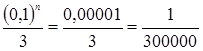 и т.д.
и т.д.
Поэтому при неограниченном увеличении n разность 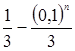 становится сколь угодно близкой к числу
становится сколь угодно близкой к числу ![]() или, как говорят, стремится к числу
или, как говорят, стремится к числу ![]() .
.
Таким образом, сумма n первых членов геометрической прогрессии 0,3; 0,03; 0,003; 0,0003; . при неограниченном увеличении п стремится к числу ![]() . Это утверждение записывают в виде равенства
. Это утверждение записывают в виде равенства
![]() .
.
Число ![]() называют суммой бесконечной геометрической прогрессии 0,3; 0,03; 0,003; 0,0003; . .
называют суммой бесконечной геометрической прогрессии 0,3; 0,03; 0,003; 0,0003; . .
Рассмотрим теперь произвольную геометрическую прогрессию ![]() у которой
у которой ![]()
Запишем формулу суммы п первых членов прогрессии: 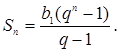
Преобразуем выражение в правой части равенства:
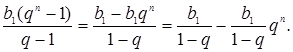
Значит, 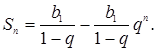
Можно доказать, что если ![]() , то при неограниченном увеличении п множитель
, то при неограниченном увеличении п множитель ![]() стремится к нулю, а значит, стремится к нулю и произведение
стремится к нулю, а значит, стремится к нулю и произведение 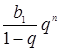 . Поэтому при неограниченном увеличении п сумма
. Поэтому при неограниченном увеличении п сумма
Другие статьи:
Особенности развития и проявления эмоций у детей с интеллектуальной
недостаточностью
Общеизвестно, что развитие личности ребёнка с нарушением интеллекта происходит по тем же законам, что и развитие нормально развивающихся детей. Но в силу интеллектуальной недостаточности оно проходит в своеобразных условиях (Л. С. Выготский, С. Я. Рубинштейн, Л. М., Шипицына, Д. Н. Исаев и др.). По данным ис ...
Задание на практику
Задание на практику по введению в специальность выдается каждому студенту индивидуально преподавателем — координатором практики, который является ведущим лектором курса «Введение в специальность». В задании указано, кто будет непосредственным руководителем практики — преподаватель, его полные фамилия, имя и ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука

