Геометрическая прогрессия

S, стремится к числу .

Число называют суммой бесконечной геометрической прогрессии

, у которой .

Это записывают так: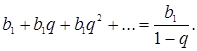

Обозначив сумму прогрессии буквой S, получим формулу

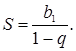(9)

Заметим, что если то сумма п первых членов геометрической прогрессии Sn при неограниченной увеличении п не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при .

Пример 1. Найдем сумму бесконечной геометрической прогрессии 12; – 4; ; ….

У этой прогрессии . Значит, условие выполняется.

По формуле (9) получим: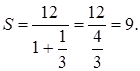

Пример 2. Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. Найдем сумму площадей всех квадратов.

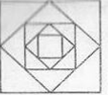
Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен . Найдем сумму этой геометрической прогрессии: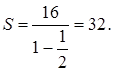

Значит, сумма площадей всех квадратов равна 32 см2.

Пример 3. Представим бесконечную десятичную периодическую дробь 0,(18) в виде обыкновенной дроби.

Запишем число 0,(18) в виде суммы: .

Слагаемые в правой части равенства – члены геометрической прогрессии, у которой первый член равен 0,18, а знаменатель равен 0,01, т.е. . Найдем сумму этой прогрессии: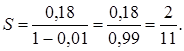

Значит,

Заметим, что аналогичным образом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь.

Другие статьи:

Минусы реформирования высшего образования
Вузы. не вошедшие в Болонскую систему, будут лишены возможности получения государственной аккредитации и финансирования из госбюджета. Научное руководство и взаимодействие с кафедрой будет доступно только магистрантам. Очень маленькое число выпускников –бакалавров смогут поступить в бесплатную магистратуру. ...

Ознакомление с животными на занятии
Развитию логического мышления детей и формированию у них нравственно-экологического отношения к животным способствует творческое рассказывание. Особенно ценны в этом отношении занятия, на которых дети придумывают рассказы на тему предложенную воспитателем. Содержание и форма проявления этого творчества могут ...

Главные разделы

• Главная
• Профессиональное самоопределение школьников
• Воспитание этнической толерантности в школе
• Понятие и технология обучения
• Образовательные технологии
• Оптимизация системы образования
• Изучение информационных технологий в школе
• Педагогика как наука