Геометрическая прогрессия
Число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
.
Умножим обе части записанного равенства на знаменатель прогрессии, получим: 
.
Вычтем из второго равенства первое и проведем упрощения:
, 
.
Масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.
Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.
Пусть дана геометрическая прогрессия 
. Обозначим сумму n первых ее членов через 
:
(5)
Умножим обе части этого равенства на q: 
Учитывая, что 
получим:
(6)
Вычтем почленно из равенства (6) равенство (5) и приведем подобные члены: 
Пусть 
, тогда 
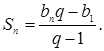(7)
Мы получили формулу суммы n первых членов геометрической прогрессии, в которой . Если 
, то все члены прогрессии равны первому члену и 
.
Заметим, что при решении многих задач удобно пользоваться формулой суммы n первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (7) вместо bn выражение 
. Получим:
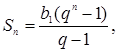если 
. (8)
Пример 1. Найдем сумму первых десяти членов геометрической прогрессии , в которой 
и 
.
Так как известны первый член и знаменатель прогрессии, то для решения задачи удобно воспользоваться формулой (8). Получим:
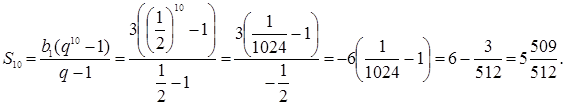
Пример 2. Найдем сумму 
, слагаемые которой являются последовательными членами геометрической прогрессии 1; x; 
; … .
Первый член прогрессии равен 1, а знаменатель ранен х. Так как 
является членом этой прогрессии с номером n, то задача состоит в нахождении суммы n первых её членов. Воспользуемся формулой (7):
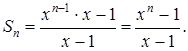
Таким oбразом, 
Умножим левую и правую части последнего равенства на 
. Получим тождество 
В частности, при 
и 
приходим к известным формулам: 
Другие статьи:
Использование игр-загадок, головоломок, кроссвордов и ребусов
в театральной деятельности детей старшего дошкольного возраста
Для построения формирующего эксперимента нам необходимо было определить степень знакомства ребят с театром и основными театральными профессиями, ребусами и кроссвордами; наличие условий в группе для использования игр-загадок, кроссвордов, ребусов в работе с детьми, отношение взрослых(педагогов и родителей) к ...
Система работы по экологическому образованию детей
дошкольного возраста
Цель экологического образования достигается по мере решения в единстве следующих задач: образовательных – формирование системы знаний об экологических проблемах современности и пути их решения; воспитательных – формирование мотивов, потребностей и привычек экологически целесообразного поведения и деятельност ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука