Геометрическая прогрессия
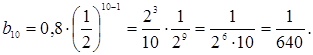
Пример 2. Найдем восьмой член геометрической прогрессии ![]() ,
,
если ![]() и
и ![]() .
.
Зная первый и третий члены геометрической прогрессии, можно найти ее знаменатель. Так как ![]() ,то
,то 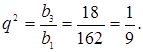
Решив уравнение ![]() найдем, что
найдем, что ![]() или
или ![]() .
.
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.
Если ![]() , то
, то 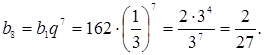
Если ![]() , то
, то 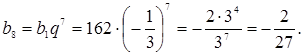
Задача имеет два решения: ![]() или
или ![]() .
.
Пример 3. После каждого, движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда после шести движений поршня, если первоначальное давление было 750 мм рт. ст.
Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление после предыдущего движения поршня умножить на 0,8.
Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде ( в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно ![]() .
.
Произведя вычисления, получим: ![]() (мм рт. ст.).
(мм рт. ст.).
Свойства геометрической прогрессии.
1. Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению соседних членов, то есть при ![]() верной является формула
верной является формула
![]() . (3)
. (3)
Если все члены геометрической прогрессии положительны, то это свойство формулируется так: каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому его соседних членов, т.е. ![]() .
.
Действительно, при ![]() имеем
имеем ![]() и
и ![]() . Перемножая почленно эти равенства, получим
. Перемножая почленно эти равенства, получим ![]() . А это и есть равенство (3).
. А это и есть равенство (3).
2. У конечной геометрической прогрессии ![]() произведение членов, равноотстоящих от ее концов, равно произведению крайних членов, т.е.
произведение членов, равноотстоящих от ее концов, равно произведению крайних членов, т.е.
![]() (4)
(4)
Действительно, в конечной геометрической прогрессии ![]() члены
члены ![]() и
и ![]() равноотстоят от концов. По формуле (2)
равноотстоят от концов. По формуле (2) ![]() и
и ![]() . Произведение этих членов
. Произведение этих членов ![]() и равно произведению крайних членов
и равно произведению крайних членов ![]() . Значит,
. Значит, ![]() . А это и есть равенство (4).
. А это и есть равенство (4).
Древняя индийская легенда рассказывает, что изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в два раза больше, т. е. 2 зерна, на третью – еще в два раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Сколько зерен должен был получить изобретатель шахмат?
Другие статьи:
Анализ результатов исследования фонематического восприятия у детей с общим
недоразвитием речи
По результатам первого этапа обследования выяснилось состояние слухового восприятия детей контрольной и экспериментальной групп (См. таблицу 1, рис. 1). Таблица 1. Анализ обследования слухового восприятия Состояние слухового восприятия Экспериментальная группа Контрольная группа человек % человек % Нарушено ...
Цели, задачи внеклассной работы по географии и основные требования к ее организации и содержанию
В условиях всеобщего среднего образования и повышения научного уровня преподавания успех обучения во многом зависит не только от выбора эффективных методов и форм обучения в классе на уроке, но и от организации внеурочной работы по предмету. Спецификой предмета является то, что именно география дает человеку ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука

