Геометрическая прогрессия

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями: 2; ; ; ; … .

Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение. Геометрической прогрессией

называется последовательность отличных от нуля чисел, в которой каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Иначе говоря, последовательность – геометрическая прогрессия, если для любого натурального n выполняются условия:

и , (1)

где q – некоторое число. Обозначим, например, через последовaтeльность натуральных степеней числа 2. В этом случае для любого натурального n верно равенство ; здесь .

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т.е. при любой натуральном n верно равенство: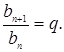

Число q называют знаменателем геометрической

прогрессии

.

Очевидно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Приведем примеры.

Пример 1. Если и q= 0,1, то получим геометрическую прогрессию: 1; 0,1; 0,01; 0,001; 0,0001;

Пример 2. Условиями и q = 3 задается геометрическая прогрессия – 2; – 6; ; – 54; – 162; . .

Пример 3. Если и , то имеем прогрессию: 4; – 12; 36; – 103; 324; … .

Пример 4. Если и q = 1, то получим геометрическую прогрессию 8; 8; 8; … .

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий, а также любой её член:

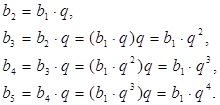
Точно так же находим, что и т. д. Вообще, чтобы найти , мы должны b1 умножить на , т. е.

(2)

Мы получили формулу n-го члена геометрической прогрессии. Докажем ее методом математической индукции.

1. Формула (2), очевидно, верна при .

2. Предположим, что она верна и при , т.е.

3. Из (1) следует , то есть формула (2) верна и при .

Из принципа математической индукции следует, что формула (2) справедлива для любого натурального п.

Что и требовалось доказать.

Приведем примеры решения задач с использованием этой формулы.

Пример 1. В геометрической прогрессии и . Найдем .

По формуле n -го члена геометрической прогрессии

Другие статьи:

Геометрическая прогрессия
Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями: 2; ; ; ; … . Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии. Определение. Геометричес ...

Использование дидактической игры в формировании представлений о геометрических фигурах и форме предмета у старших дошкольников в педагогической практике
дидактический дошкольник геометрический игра С середины прошлого века дидактическая игра начал успешного использоваться в обучении детей до школы. В исследованиях отечественных педагогов и психологов подчеркивалась многоплановая взаимосвязь и взаимовлияние игры и обучения. В дидактических играх актуализирует ...

Главные разделы

• Главная
• Профессиональное самоопределение школьников
• Воспитание этнической толерантности в школе
• Понятие и технология обучения
• Образовательные технологии
• Оптимизация системы образования
• Изучение информационных технологий в школе
• Педагогика как наука