Методические рекомендации к урокам решения задач по теме «Арифметическая и геометрическая прогрессии»
Решение. По условию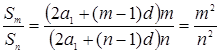 
.
Из последнего равенства получаем:
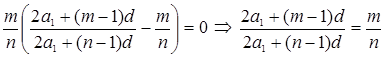, так как 
.
"Альянс Климат": кондиционеры Quattroclima купить - klimat-urala.ru
Дальнейшие преобразования приводят к уравнению
, или 
.
Если 
, то 
и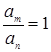 
.
Пусть 
, тогда 
, причем из условия ясно, что 
. Найдем требуемое отношение: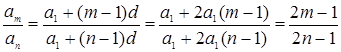 
.
Ответ: 
.
Другие примеры нестандартных задач предложены в §7.
На уроках решения задач по теме «Арифметическая и геометрическая прогрессии» полезно рассмотреть старинные задачи, которые также способствуют активизации познавательной деятельности учащихся и являются бесспорным украшением этих уроков. Примеры таких задач предложены в §7.
Другие статьи:
Задание на экономико-управленческую практику
Для прохождения экономико-управленческой практики в установленные сроки студент подготавливает ряд определенных документов. На предварительном этапе он подает заявление на имя заведующего выпускающей кафедры с просьбой о направлении на практику с указанием организации и подразделения. На выпускающей кафедре ...
Анализ результатов опытно - эмпирического исследования по социальной
адаптации детей младшего школьного возраста разведенных родителей
В ходе выполнения нашего исследования, для определения уровня социальной адаптации детей младшего школьного возраста разведенных родителей была проведена работа на базе школы № 22 г. Абакана с учащимися 4 класса, в количестве - 17 человек. Была проведена диагностика на выявление межличностных отношений в кла ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука