Методические рекомендации к урокам решения задач по теме «Арифметическая и геометрическая прогрессии»
3. Задачи с практическим и экономическим содержанием на прогрессии.
Рассмотрим несколько примеров решения таких задач.
Задача 1. В сберегательный банк внесли вклад в 10000 руб. с доходом 2% годовых. Какую сумму выплатит сберегательный банк вкладчику через 4 года?
Решение. Сбербанк за один год выплатит 
, где 
– вклад, q – процентная ставка. За 2 года 
, но 
, следовательно, 
.
Легко убедиться, что за 3 года 
, …, за n лет 
.
По этой формуле определим сумму, которую сбербанк выплатит вкладчику по истечении четырех лет:
.
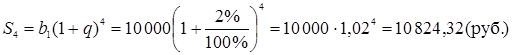Ответ: 
.
Задача 2. Бегун за первую минуту бега пробежал 400 м, а в каждую следующую минуту пробежал на 5 м меньше, чем в предыдущую. Какой путь пробежал он за 1 ч?
Решение. За первую минуту бегун пробежал 400 м, за вторую – 395 м, за третью – 390 м и т. д. Числа 400, 395, 390, … образуют арифметическую прогрессию, у которой 
, 
. Путь за 1 ч, т. е. за 60 мин, равен сумме первых шестидесяти членов прогрессии. Увидев формулу 
, получим: 
.
Итак, за 1 ч бегун пробежал 15 км 150 м.
Ответ: 15 км 150 м.
Другие примеры задач этого типа предложены в §7 приложении 4.
4.Нестандартные задачи на прогрессии.
Учащиеся затрудняются в решении задач на прогрессии с буквенными данными. Но эти задачи часто встречаются на вступительных экзаменах в вузы. Поэтому школьников следует учить решению таких задач не только на внеклассных занятиях, но и на уроках, что, естественно, способствует активизации деятельности учащихся на уроках–практикумах. Осуществить такое обучение легче всего с помощью целой подборки заданий. Далее предлагается такая подборка.
Задача 1. Найдите сумму 
членов арифметической прогрессии, если сумма первых 
членов этой прогрессии равна 
.
Решение. Преобразуем искомую сумму:
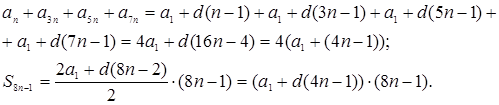
По условию 
, отсюда 
.
Ранее мы доказали, что 
.
Из последних двух равенств следует: 
.
Ответ: 
.
Задача 2. В арифметической прогрессии 
. Найдите отношение 
к 
.
Другие статьи:
Требования к знаниям и умениям учащихся по линии информационных технологий
Учащиеся должны знать: ● способы представления символьной информации в памяти ЭВМ (таблицы кодировки, текстовые файлы); ● назначение текстовых редакторов (текстовых процессоров); ● основные режимы работы текстовых редакторов (ввод, редактирование, печать, орфографический контроль, поиск и з ...
Состояние чтения учащихся массовой общеобразовательной школы
Количественные данные о состоянии качества чтения представлены в таблице 1 Оценка качества чтения у учащихся 3-го класса массовой общеобразовательной школы № Имя 1 2 3 4 5 6 7 8 9 10 11 Баллы 1 Снежана К. 1 5,0 2 Даня В. 1 1 ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука