Методические рекомендации к урокам решения задач по теме «Арифметическая и геометрическая прогрессии»
Рассмотрим несколько примеров решения таких задач.
Задача 1. Дано: 
. Найти 
.
Решение.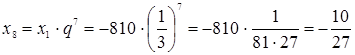 
.
Ответ: 
[25].
Задача 2. Дано: 
, 
. Найти 
.
Решение.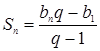 
; 
;
.
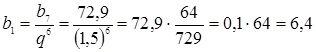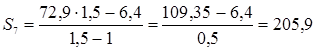Ответ: 205,9 .
Упражнений такого вида достаточно в учебных пособиях для девятого класса. Они являются самыми простыми и рассматриваются на первых уроках решения задач на прогрессии.
2. Задачи, в которых по заданной зависимости между членами арифметической и геометрической прогрессий (или одной из них), требуется найти сами прогрессии.
Рассмотрим несколько примеров решения таких задач.
Задача 1. В арифметической прогрессии 
выполняется 
, 
. Найдите 
и 
.
Решение: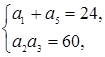
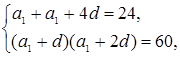
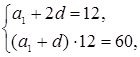
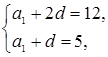
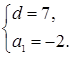
Ответ: 
, 
[1].
Задача 2. Дано: 
– арифметическая прогрессия,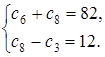 
Найдите 
и
d.
Решение.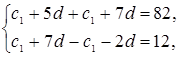 
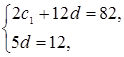
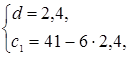
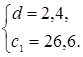
Ответ: 
, 
.
При решении задач этого вида полезно разнообразить содержание, рассмотрев, например, случай, когда разность (знаменатель) прогрессии есть иррациональные числа. Часто очень помогает решению задач использование характеристических свойств прогрессий, доказательство которых само по себе составляет прекрасную задачу.
Другие статьи:
Диагностика обучения школьников
Диагностика учебного процесса в последнее время имеет все большее значение в обучении школьников. В настоящее время основной упор делается даже не на сам контроль знаний как таковой, а на то, каковы общие результаты процесса обучения, на то, что надо сделать, чтобы повысить уровень обучаемости учеников. Диаг ...
Использование дидактической игры в формировании представлений
о геометрических фигурах и форме предмета у старших дошкольников в
педагогической практике
дидактический дошкольник геометрический игра С середины прошлого века дидактическая игра начал успешного использоваться в обучении детей до школы. В исследованиях отечественных педагогов и психологов подчеркивалась многоплановая взаимосвязь и взаимовлияние игры и обучения. В дидактических играх актуализирует ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука