Применение микрокалькуляторов в начальных классах

Педагогика как наука » Применение микрокалькуляторов в начальных классах

Страница 4

Примеры

Задача 1. Найти рациональные числа n и k, такие, что

Решение. При помощи микрокалькулятора последовательно находим:

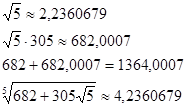
Сравнив первое и последнее из этих неравенств, получаем, что k=1 и n=2, т.е.

Использование микрокалькулятора на уроке в начальной школе. =2+

Задача 2. Сумма трех целых чисел равна a,b,c нулю. Доказать, что число 2a2+2b4+2c4 является квадратом целого числа.

Решение. Попытаемся получить гипотезу о каких-либо свойствах данного выражения путем рассмотрения частных случаев.

Если, например, a=1, b=2, c=-3 b и данное выражение равно 196=142. Если a=2, b=3, c=-5 и данное выражение равно 1444=382.

Но как связаны значения a,b,c с основанием 142, 382? Легко заметить, что 14=12+22+(-3)2, 38=22+32+(-3)2. Итак появляется гипотеза, что 2(a2+b4+c4)= (a2+b2+c2)2

Если a+b+c=0. Полученная в результате математического эксперимента гипотеза легко доказывается.

Задача 3. Решить уравнение

Решение. Отрицательных корней не имеет, потому что на (-∞;0) функция

P(x)= убывает, K(x)=3∙2x возрастает и P(0)>K(0).Для получения гипотезы о числе корней данного уравнения составляем таблицу функций P(x) и K(x):

P(x)

K(x)

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

2.2

2.4

2.6

2.8

5.954

5.956

5.961

5.971

5.984

6.018

6.039

6.062

6.087

6.113

6.141

6.169

6.197

6.226

6.255

3.45

3.95

4.55

5.22

6.89

7.92

9.09

10.4

13.8

15.8

18.2

20.9

Теперь можно сделать предположение, что если x>2, то (это неравенство легко доказывается при помощи производной). После этого становиться ясным, что все корни данного уравнения принадлежат [0;2]. Число 1 является корнем уравнения.

Страницы: 1 2 3 4

Другие статьи:

Состояние вопроса в современной российской школе
Естествознание - одно из звеньев в системе общего образования. Как многократно подчеркивал в своих трудах русский ученый, методист Н.М. Верзилин, курс естествознания имеет важное значение в развитии и воспитании подрастающего поколения, в совершенствовании общей культуры школьников, развитии творческой лично ...

Методика применения «опорных конспектов» в общеобразовательной школе
Понятие опорного конспекта прочно вошло в педагогическую литературу, начиная с работ донецкого учителя-новатора Шаталова. Здесь опорный конспект по физике понимается расширительно в той мере, в какой он может заменить минимальный конспект для учащихся. Опорный конспект представляет собой наглядную схему, в к ...

Применение микрокалькуляторов в начальных классах

Главные разделы