Внеклассная работа по теме «Арифметическая и геометрическая прогрессии»

, .

Первое уравнение можно переписать в виде , а второе – в виде , т.е. . Делением первого уравнения на второе получим , .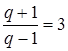

Следовательно, . Значит, данное число равно 842.

Однако можно пойти по другому пути: так как цифры числа образуют геометрическую прогрессию, само число больше 594, то в нашем распоряжении только три возможности: 931, 842 и 964. Второе и третье из этих чисел нужно отбросить, т.к. и . Остается убедиться, что для числа 842 все условия задачи выполнены.

Требование, чтобы числа , , образовали арифметическую прогрессию, при таком решении оказывается лишним.

Ответ: 842 .

Задача 9. Имеющиеся в совхозе комбайны, работая вместе, могут убрать урожай за одни сутки. Однако по плану комбайны возвращались с других полей и вступали в работу последовательно: в первый час работал лишь один комбайн, во второй – 2, в третий – 3 и т.д. до тех пор, пока не начали работать все комбайны, после чего в течение нескольких часов перед завершением уборки урожая действовали все комбайны. Время работы по плану можно было сократить на 6 ч, если бы с самого начала уборки постоянно работали все комбайны, за исключением пяти. Сколько было комбайнов в совхозе?

Решение. Всю работу следует принять за 1. Чтобы использовать условия задачи, нужно знать производительность одного комбайна. Однако нам не известно, сколько часов перед завершением работы по плану все комбайны работали вместе. Поскольку удобнее вводить одноименные неизвестные, то эту величину обозначим через , а через обозначим количество часов, необходимых одному комбайну, чтобы убрать весь урожай. Тогда производительность комбайна будет равна .

В задаче спрашивается, сколько комбайнов было в совхозе. Эту величину обозначим через . Условия задачи позволяют составить три уравнения. При этом левая часть уравнения, соответствующего работе по плану, представляет собой сумму членов арифметической прогрессии. При решении системы уравнений нужно исключить и .

Итак, пусть в совхозе было комбайнов, один смог бы убрать весь урожай за ч. непрерывной работы, и при работе по плану все комбайны одновременно находились в поле ч. Так как все комбайны могли справиться с уборкой за 24 ч., а производительность одного комбайна , то , т.е. .

Другие статьи:

Личностно-развивающий потенциал урока как предмет специальной проектировочной деятельности учителя
Он реализуется с учетом возрастных особенностей школьников. Итак, урок может содержать в себе: - включение в содержание урока специально подобранного материала, позволяющего ученикам выразить свое отношение к изучаемому; - организация деятельности учащихся, имплицитно содержащая возможность рефлексии, самооц ...

Научно-теоретические основы развития сюжетно-ролевых игр старших дошкольников
Проблема развития игровой деятельности в исследованиях отечественных и зарубежных психологов и педагогов Игра представляет собой особую деятельность, которая расцветает в детские годы и сопровождает человека на протяжении всей его жизни. Неудивительно, что проблема игры привлекала и привлекает к себе внимани ...

Главные разделы

• Главная
• Профессиональное самоопределение школьников
• Воспитание этнической толерантности в школе
• Понятие и технология обучения
• Образовательные технологии
• Оптимизация системы образования
• Изучение информационных технологий в школе
• Педагогика как наука