Внеклассная работа по теме «Арифметическая и геометрическая прогрессии»
Тогда 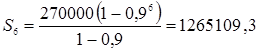 (руб.).
(руб.).
Ответ: 1265109,3 руб.
Далее рассмотрим случай, когда количество банков в системе будет увеличиваться неограниченно. Конечно в конкретной банковской системе так не бывает, но математические методы как раз и сильны тем, что с их помощью можно рассматривать предельные возможности, которые не реализуются ни при каком значении п, т.е. можно заглянуть туда, где бессилен любой опыт. Из формулы 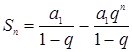 при
при ![]() следует, что при больших значениях п величина
следует, что при больших значениях п величина ![]() мала, и ею можно пренебречь. Тогда мы получаем формулу
мала, и ею можно пренебречь. Тогда мы получаем формулу 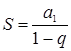 .
.
Это знакомая ученикам формула для нахождения суммы членов бесконечно убывающей геометрической прогрессии. Ее экономический смысл состоит в том, что при фиксированных значениях ![]() и
и ![]() она указывает границу, предельные возможности системы. Сколько банков мы бы не включали в нее, выдать кредитов на сумму, равную или большую числа
она указывает границу, предельные возможности системы. Сколько банков мы бы не включали в нее, выдать кредитов на сумму, равную или большую числа 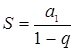 невозможно. Множитель
невозможно. Множитель 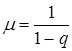 экономисты называют мультипликатором (от английского слова multiply – умножать). В нашем случае мультипликатор показывает, во сколько раз увеличивается величина начального кредита при рассмотрении бесконечной системы банков. Так, при
экономисты называют мультипликатором (от английского слова multiply – умножать). В нашем случае мультипликатор показывает, во сколько раз увеличивается величина начального кредита при рассмотрении бесконечной системы банков. Так, при ![]() и
и ![]() имеем
имеем 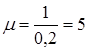 и
и ![]() – этот результат мы уже получили выше.
– этот результат мы уже получили выше.
Если на занятии осталось время, то можно рассмотреть решение некоторых обратных задач. При его отсутствии такие задачи можно задать на дом.
Задача 3. В первый банк некоторой системы банков внесен вклад размером С руб. Процентная ставка обязательных резервов составляет ![]() %. Сколько банков должно быть в системе, чтобы их суммарная возможность кредитования была не менее заданной величины
%. Сколько банков должно быть в системе, чтобы их суммарная возможность кредитования была не менее заданной величины ![]() ? Решите задачу при следующих данных:
? Решите задачу при следующих данных:
1) ![]() руб.,
руб., ![]() руб.;
руб.;
2) ![]() руб.,
руб., ![]() руб.;
руб.;
3) ![]() руб.,
руб., ![]() руб.;
руб.;
4) ![]() руб.,
руб., ![]() руб.
руб.
Решение. 1) Искомое число п находим из условия 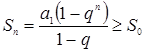 , где
, где ![]()
![]()
![]()
Другие статьи:
Коррекционная работа по развитию зрительного восприятия детей с нарушением
зрения
Обучение и воспитание в детских садах для детей с косоглазием и амблиопией направлено на раннюю коррекцию и компенсацию вторичных отклонений в развитии детей, осуществление лечебно-восстановительной работы по исправлению косоглазия и амблиопии, а также успешную подготовку детей к обучению в школе. Успешность ...
Интересы и способности подростков
"Очень важно верить в способности ребенка. Из позитивного окружения, которое вы создаете, он возьмет то, что ему необходимо. Для него ваша вера в его силы - достойная уважения предпосылка. Взрослый должен помогать, но не тянуть или толкать." В современных требованиях к школе четко прослеживается ва ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука

