Внеклассная работа по теме «Арифметическая и геометрическая прогрессии»
Если в (1) раскрыть скобки, а затем вынести за скобки а, то
(1')
Сравним с уравнением (3): 
.
Первое из уравнений (2) можно переписать так:
.
Раскроем скобки и решим систему, состоящую из уравнения, полученного в результате, и из уравнения (1'):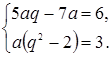 
Из первого уравнения получаем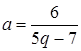 
. Подставим во второе. После преобразований получим квадратное уравнение 
, откуда 
. Второй корень посторонний, так как тогда всем братьям одинаковое количество лет и никто из них не может через три года стать вдвое старше другого.
Итак, первому брату 12 лет, второму – 18 лет, а третьему – 27 лет.
Ответ: 12, 18, 27 лет [4].
Задача 6. Докажите, что если положительные числа 
образуют арифметическую прогрессию, то числа 
также образуют арифметическую прогрессию.
Решение. По условию 
, отсюда 
. Рассмотрим разности: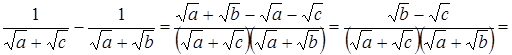 
.
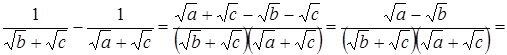
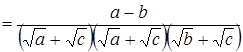Отсюда следует, что разность между вторым и первым членами данной последовательности равна разности между ее третьим и вторым членом, а это и значит, что числа образуют арифметическую прогрессию.
Что и требовалось доказать.
В качестве заданий для индивидуальной работы можно предложить учащимся следующие задачи.
1. При каких значениях x и y последовательность 
, 
, 
, где 
, 
, 
, является одновременно арифметической и геометрической прогрессией? Отв. 
.
2. Найти трехзначное число, цифры которого образуют арифметическую прогрессию и которое делится на 45. Отв. 135; 630; 765 [39].
3. Три отличных от нуля действительных числа образуют арифметическую прогрессию, а квадраты этих чисел, взятые в том же порядке, образуют геометрическую прогрессию. Найти всевозможные знаменатели этой геометрической прогрессии. Отв. 1; 
; 
.
Другие статьи:
Особенности мотивационной готовности к обучению старших дошкольников
В структуре стартовой готовности к обучению в школе это наиболее важное качество. По определению мотив — это внутреннее побуждение к активности. В качестве мотивов выступают потребности, интересы, убеждения, представления о нормах и правилах поведения, принятых в обществе, и др. В основе любого действия или ...
Особенности реализации учебных программ в практической деятельности
студентов
Государственные образовательные стандарты, действующие в практике работы образовательных учреждений среднего и высшего профессионального образования, должны постоянно совершенствоваться с учетом мнения руководителей практического здравоохранения, являющихся "заказчиками" для образовательных учрежде ...
Главные разделы
- Главная
- Профессиональное самоопределение школьников
- Воспитание этнической толерантности в школе
- Понятие и технология обучения
- Образовательные технологии
- Оптимизация системы образования
- Изучение информационных технологий в школе
- Педагогика как наука