Внеклассная работа по теме «Арифметическая и геометрическая прогрессии»

Факультативное занятие №2. Старинные задачи по теме «Арифметическая и геометрическая прогрессии»

Старинные задачи способствуют развитию интереса учащихся к прогрессиям, а также позволяют разнообразить перечень задач, предлагаемых для решения школьникам, в итоге активизировав их познавательную деятельность.

Задача 1. Древнейшая задача на прогрессии – не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце 19 века, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, возможно, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая:

Сто мер хлеба необходимо разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Решение. Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член х, разность у. Тогда доля первого – х, второго – (х+у), третьего – (х+2у), четвертого – (х+3у), пятого – (х+4у).

На основании условий задачи составляем следующие два уравнения:

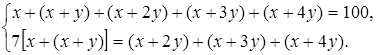
После упрощений первое уравнение получает вид х+2у=20, а второе: 11х=2у. Решив эту систему, получаем: , .

Значит, хлеб должен быть разделен на следующие части: , ,

Ответ: .

Задача 2. В огороде 30 грядок, каждая длиной 16 м и шириной 2,5 м. Поливая грядки, огородник приносит ведра с водой из колодца, расположенного в 14 м от края огорода, и обходит грядки по меже, причем воды, приносимой за один раз, достаточно для поливки только одной грядки. Какой длины путь должен пройти огородник, поливая весь огород? Путь начинается и кончается у колодца.

Решение. Для поливки первой грядки огородник должен пройти путь 14+16+2,5+16+2,5+14=65(м.). При поливке второй он проходит 14+2,5+16+2,5+16+2,5+2,5+14=65+5=70(м.).

Каждая следующая грядка требует пути на 5 м длиннее предыдущей. Имеем прогрессию: 65; 70; 75; …; 65+5×29.

Сумма её членов равна (м.).

Огородник при поливке всего огорода проходит путь в 4,125 км.

Ответ: 4,125 км.

Задача 3. Садовник продал первому покупателю половину всех своих яблок и еще пол-яблока, второму покупателю – половину оставшихся и еще пол-яблока, третьему – половину оставшихся и еще пол-яблока и т. д. Седьмому покупателю он продал половину оставшихся яблок и еще пол-яблока; после этого яблок у него не осталось.

Другие статьи:

Характеристика программы “Начала алгебры” для 6-го класса
Основным результатом обучения в среднем звене должна являться математическая грамотность учащихся как общекультурное умение, в которое входит : владение основными понятиями и методами изучения математических объектов (такими как обобщение, спецификация, аналогия, распространение, систематизация и др.); умени ...

Роль музыкального воспитания в развитии эмоций у детей с интеллектуальной недостаточностью
Упоминание о целительном и коррекционно-развивающем воздействии музыки уходит корнями в древние времена. Виднейшие учёные Пифагор, Аристотель, Платон указывали на лечебное и профилактическое воздействие музыки. Они считали, что музыка устанавливает пропорциональный порядок и гармонию во Вселенной, в том числ ...

Главные разделы

• Главная
• Профессиональное самоопределение школьников
• Воспитание этнической толерантности в школе
• Понятие и технология обучения
• Образовательные технологии
• Оптимизация системы образования
• Изучение информационных технологий в школе
• Педагогика как наука